dda_maths.c File Reference

Mathematic algorithms for the digital differential analyser (DDA). More...

#include "dda_maths.h"
#include <stdlib.h>
#include <stdint.h>

Functions
const int32_t	muldivQR (int32_t multiplicand, uint32_t qn, uint32_t rn, uint32_t divisor)
	Integer multiply-divide algorithm.
uint32_t	approx_distance (uint32_t dx, uint32_t dy)
	linear approximation 2d distance formula
uint32_t	approx_distance_3 (uint32_t dx, uint32_t dy, uint32_t dz)
	linear approximation 3d distance formula
uint16_t	int_sqrt (uint32_t a)
	integer square root algorithm
const uint8_t	msbloc (uint32_t v)
	crude logarithm algorithm

---

Detailed Description

Mathematic algorithms for the digital differential analyser (DDA).

---

Function Documentation

uint32_t approx_distance	(	uint32_t	dx,
		uint32_t	dy
	)

linear approximation 2d distance formula

Parameters:

	dx	distance in X plane
	dy	distance in Y plane

Returns:

3-part linear approximation of

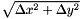
see http://www.flipcode.com/archives/Fast_Approximate_Distance_Functions.shtml

Referenced by dda_create().

uint32_t approx_distance_3	(	uint32_t	dx,
		uint32_t	dy,
		uint32_t	dz
	)

linear approximation 3d distance formula

Parameters:

	dx	distance in X plane
	dy	distance in Y plane
	dz	distance in Z plane

Returns:

3-part linear approximation of

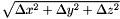
see http://www.oroboro.com/rafael/docserv.php/index/programming/article/distance

Referenced by dda_create().

uint16_t int_sqrt

(

uint32_t

a

)

integer square root algorithm

Parameters:

a

find square root of this number

Returns:

sqrt(a - 1) < returnvalue <= sqrt(a)

see http://www.embedded-systems.com/98/9802fe2.htm

const uint8_t msbloc

(

uint32_t

v

)

crude logarithm algorithm

Parameters:

v

value to find of

Returns:

floor(log(v) / log(2))

Referenced by dda_create().

const int32_t muldivQR	(	int32_t	multiplicand,
		uint32_t	qn,
		uint32_t	rn,
		uint32_t	divisor
	)

Integer multiply-divide algorithm.

Returns the same as muldiv(multiplicand, multiplier, divisor), but also allowing to use precalculated quotients and remainders.

Parameters:

	multiplicand
	qn	( = multiplier / divisor )
	rn	( = multiplier % divisor )
	divisor

Returns:

rounded result of multiplicand * multiplier / divisor

Calculate a * b / c, without overflowing and without using 64-bit integers. Doing this the standard way, a * b could easily overflow, even if the correct overall result fits into 32 bits. This algorithm avoids this intermediate overflow and delivers valid results for all cases where each of the three operators as well as the result fits into 32 bits.

Found on http://stackoverflow.com/questions/4144232/ how-to-calculate-a-times-b-divided-by-c-only-using-32-bit-integer-types-even-i